• Elevation and perspective
• Perspective: the vanishing point
• Perspective: the horizon line
• Perspective: proportions

Elevation and perspective

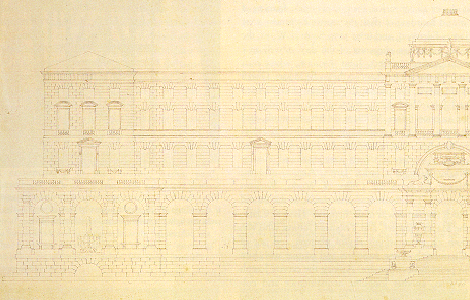
Somerset House

Chambers, elevation for the river front of Somerset House (Victoria and Albert Museum Picture Library)
[click on the picture to enlarge it]

An architect would prepare his designs as plans and elevations: in an elevation, the house would be viewed from the front ; the parallel horizontal lines of the bands and cornices between the storey would remain drawn as horizontals.

View of Somerset House

Jean-Louis Desprez, View of Somerset House (Yale Center for British Art/ The Bridgeman Art Library)
[click on the picture to enlarge it]

A draughtsman would prefer an oblique perspective view: the house is viewed from the angle, the parallel lines of the storeys are drawn as obliques converging towards a vanishing point.

Top of Page

Perspective: the vanishing point

Top of Page

Perspective: the horizon line

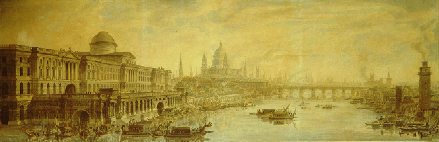
View of Somerset House

Jean-Louis Desprez, View of Somerset House (Yale Center for British Art/ The Bridgeman Art Library)
[click on the picture to enlarge it]

Somerset House

Edward Dayes, Somerset House, c.1790 (The Courtauld Gallery, London/ Bridgeman Art Library)
[click on the picture to enlarge it]

Draughtsmen could select a fairly high point of view and horizon line (where horizontal receding lines converge), like Desprez, who placed his supposed observer at the height of the terrace or they selected a low point of view and horizon line, like Dayes, who placed them just above the water, so that the building dominates his supposed observer placed almost as if he were in a boat on the Thames.

Dayes also practised frontal perspective, for instance in his View of Hanover Square

Top of Page

Perspective: proportions

Pulteney Bridge: Turner’s problem

The painter J. M. W. Turner, best known for his romantic landscape paintings, used Pulteney Bridge (Bath) in his lectures as Professor of Perspective at the Royal Academy, to introduce the students to the problem of the division of a projected line according to given proportions.

Adam’s buildings, characterized by geometrical shapes of regular proportions, were particularly well suited for this demonstration.

Robert Adam, design for Pulteney Bridge (c. 1770, By courtesy of the Trustees of Sir John Soane’s Museum)

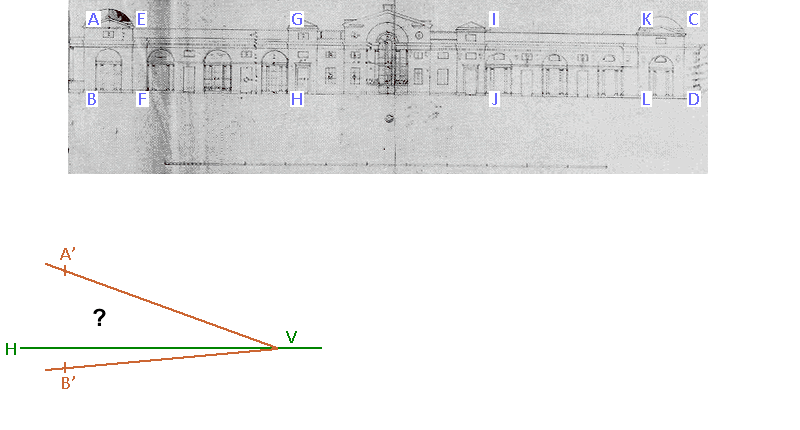
The problem: Suppose we have the elevation of a building ABCD divided into several sections having BF, FH, HJ, JL, LD as measurements,and we wish to project it in oblique view so that the horizontals AC and BD become receding lines starting from A’ and B’ and converging on a horizon line on vanishing point V, how shall we space the verticals which are the projection of AB, EF, GH, IJ, KL, CD, so that the proportions between BF, FH, HJ, JL, LD are preserved?

[click on the picture to enlarge it]

Robert Adam, design for Pulteney Bridge (c. 1770, By courtesy of the Trustees of Sir John Soane’s Museum)

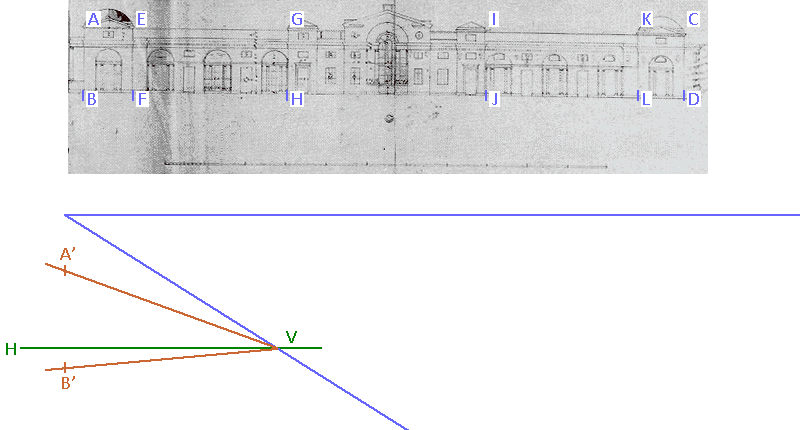
First we establish a horizontal “measuring line” above the proposed projection and a receding line towards V...

[click on the picture to enlarge it]

Robert Adam, design for Pulteney Bridge (c. 1770, By courtesy of the Trustees of Sir John Soane’s Museum)

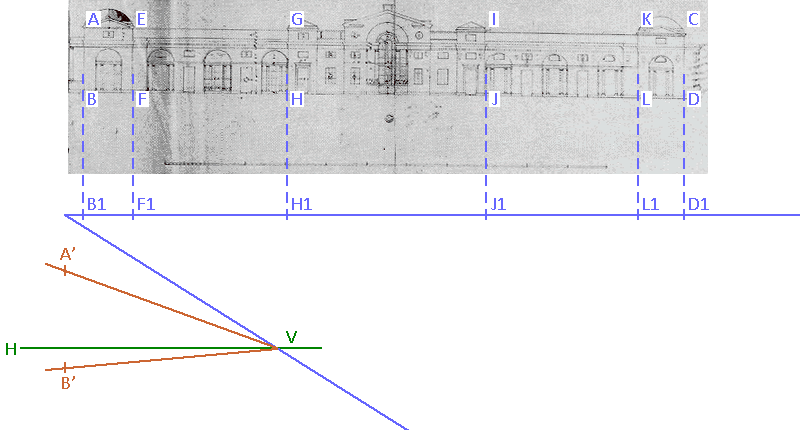
...then from the division markers B, F, H, J, L, D, we drop verticals on the measuring line, which gives points B1, F1, H1, J1, L1, D1 ...

[click on the picture to enlarge it]

Robert Adam, design for Pulteney Bridge (c. 1770, By courtesy of the Trustees of Sir John Soane’s Museum)

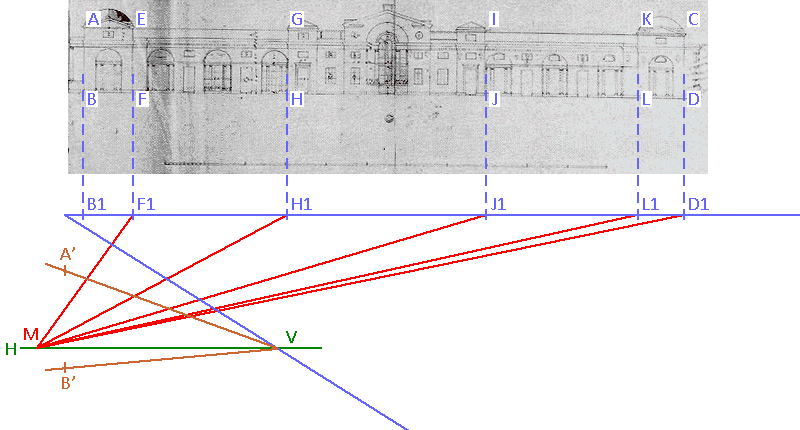
...then from measuring point M on the horizon line draw MF1, MH1, MJ1, ML1, MD1...

[click on the picture to enlarge it]

Robert Adam, design for Pulteney Bridge (c. 1770, By courtesy of the Trustees of Sir John Soane’s Museum)

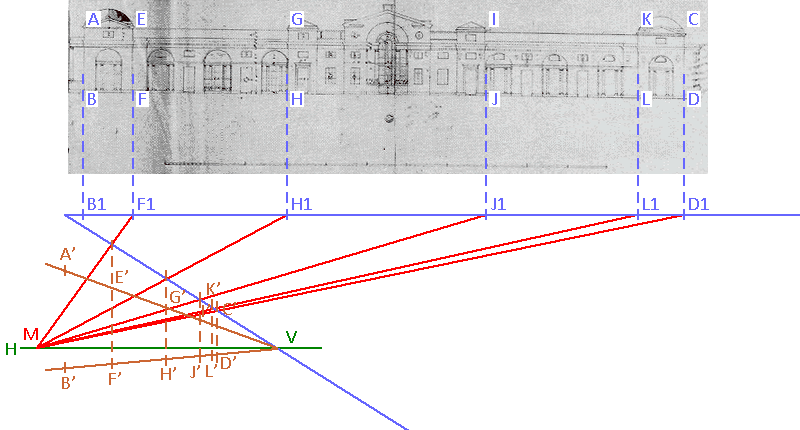
...and at the point where they cross the oblique B1 V draw verticals which are the projections of the verticals of the elevation.

[click on the picture to enlarge it]

Robert Adam, design for Pulteney Bridge (c. 1770, By courtesy of the Trustees of Sir John Soane’s Museum)

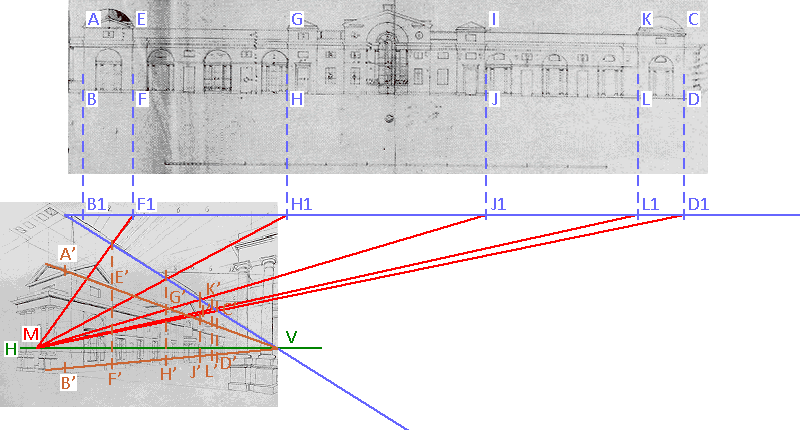
We can now draw the rest of the bridge in this wireframe structure...

[click on the picture to enlarge it]

Robert Adam, design for Pulteney Bridge (c. 1770, By courtesy of the Trustees of Sir John Soane’s Museum)

This is Turner’s finished drawing (c.1815, Turner Bequest CXCV 113)

[click on the picture to enlarge it]